-
그래프 VS 트리 / 실생활 예시개발 2022. 5. 24. 21:27
❗️그래프의 방향 VS 무방향 / 트리의 종류들을 나누어서 설명하지는 않습니다.
각각의 자세한 설명은 여기에서 각각 확인하실 수 있습니다.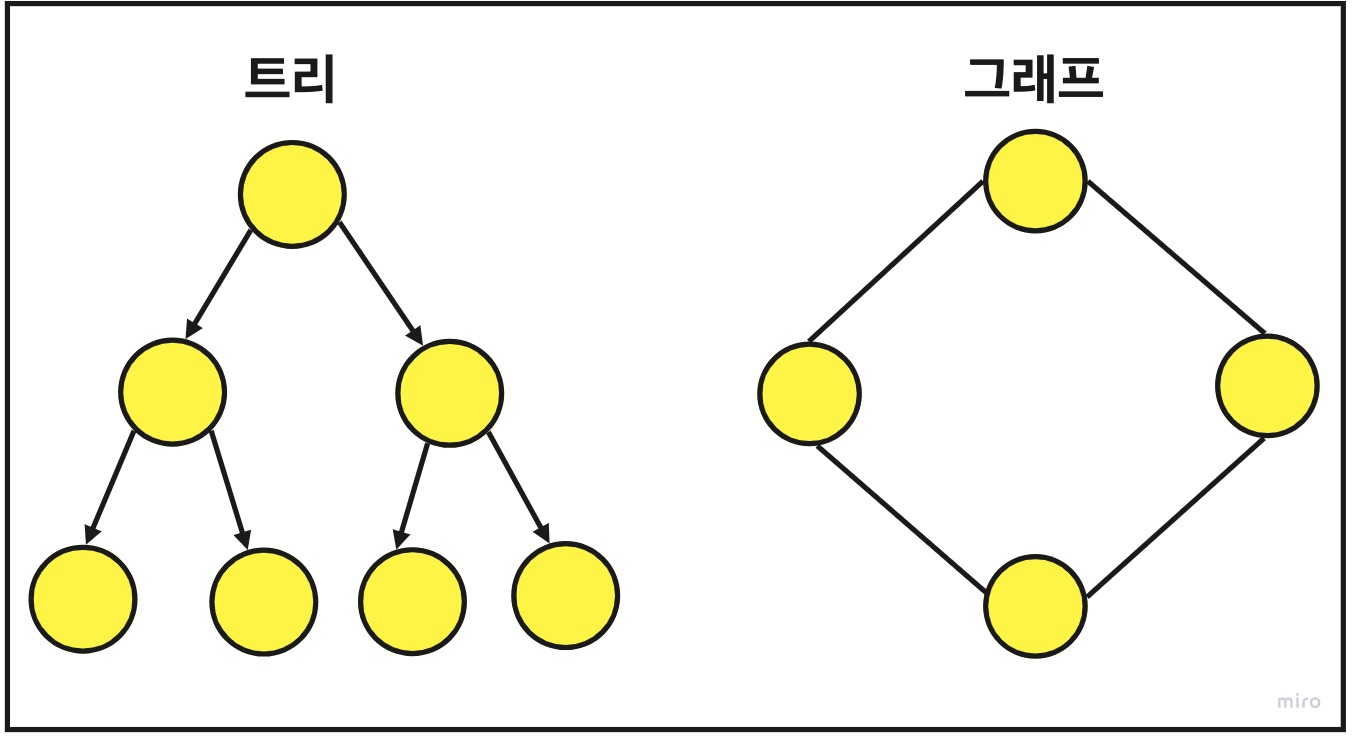
트리와 그래프 참고 이미지 위의 그림을 통해 그래프와 트리가 어떻게 생겼는지 눈으로 먼저 익혀보고, 쉽게 받아들이고 공감할 수 있도록 우리의 실생활에서
어떤 경우와 관련이 있는지 그림과 함께 연관 지어 설명해 보도록 하겠습니다.
먼저, 그림 그대로를 설명해 보면 트리는 방향(화살표)이 있고, 그래프는 방향(화살표)이 없이 선으로만 이어져 있는 것을 볼 수 있습니다.
방향이 있는 것으로 보아 트리는 계층형 모델이라는 것을 알 수 있을 것이고, 그래프는 양방향이라는 것을 알 수 있을 것이고 트리는 동그라미와 동그라미 사이에 반드시 1개의 경로만 가지고 있지만 그래프는 화살표가 따로 없는 것으로 보아 동그라미와 동그라미(이하 노드) 사이에 2개(N개)의 경로(이하 간선)를 가지고 있다는 것을 알 수 있습니다.
정리하면 트리는 노드가 N개이면 간선은 N-1개이며 비순환이기 때문에 사이클이 존재하지 않고 맨 위에 있는 노드가 루트 노드입니다.
그래프는 방향성이 없고 계층형 모델이 아니기 때문에 루트 노드의 개념이 없습니다.
그래프는 2개 이상의 경로가 가능하여 N개의 간선을 가질 수 있으며 방향성이 없고 계층형 모델이 아니기 때문에 루트 노드의 개념이 없습니다. 하지만 때에 따라 그래프도 순환/비순환 구조가 가능하며 방향성도 무방향/방향/양방향이 가능합니다.
트리보다 관계가 좀 더 자유로워서 좋은 것 같기도 하지만 방향성이 없어서 뒤죽박죽 복잡할 것 같다는 느낌이 들기도 하네요!
💡 실생활과 연관 있는 경우 알아보기
그래프
🚘 네비게이션 / 길찾기
서울에 사는 A가 차를 타고 대전에 사는 B를 태워서 부산에 사는 C에게 놀러 가려고 합니다.
이 경우를 그래프로 나타내면 다음과 같습니다.
참고 이미지 - 노드 : 서울, 대전, 부산
- 간선
- 서울 - 대전
- 대전 - 부산
- 부산 - 서울
부산에서 서울로 바로 갈 수도 있고, 서울에서 부산으로 바로 갈 수도 있으며, 대전에서 서울, 서울에서 대전 이렇게 양방향으로 모두 이동이 가능합니다.꼭! 대전을 들린 후에 부산으로 가야만 한다면 방향이 있는 경우가 될 수도 있겠죠.
👥 SNS 팔로우 / 친구 추천
페이스북이나 인스타그램 등등 SNS를 하다 보면 친구의 친구가 알 수도 있는 사람 또는 친구 추천에 뜨기도 하고 팔로우 하지 않았는데도 팔로우 한 사람을 통해 건너건너 다른 사람의 피드를 볼 수 있는 경우를 경험한 적이 있을 거예요.
이 또한 그래프의 특성을 이용한 경우인데요, 그림을 통해서 나타내면 다음과 같습니다.
참고 이미지 A는 B를 팔로우하고 있고, B는 A, C, D와 서로 팔로우 하고 있습니다.
D는 A와 B를 팔로우하고 있으며 C는 B만 팔로우하고 있는 그림입니다.
A는 C와 직접적으로 팔로우를 하지 않았지만(연결된 간선이 없기 때문) B를 통해서 C를 건너 볼 수 있습니다.
D 또한 C와 직접적으로 팔로우 하지 않았지만 A를 건너 B를 건너 C를 볼 수도 있고, B를 통해서도 C를 볼 수 있습니다.
🔎 검색 엔진
유튜브나 네이버 같은 곳에서 어떠한 키워드를 검색하면 연관검색어에 비슷한 검색어나 관련된 콘텐츠들이 연관 지어 뜨는 것을 본 적이 있으실 거예요. 요즘 검색 엔진은 똑똑해서 내가 최근에 관심 있게 검색하는 것이 무엇인지 파악하고 관련된 콘텐츠나 광고들을 귀신같이 알고 여기저기 띄워주기도 하죠! 이것도 그래프의 특성을 이용한 사례입니다.

참고 이미지
포도를 검색했다고 해서 포도만 검색되는 것이 아니라 연관 검색어나 관련 콘텐츠에 포도와 관련된 다양한 키워드가 포함된 콘텐츠들이 같이 노출되고 있습니다.마찬가지로 청포도, 과일, 거봉 등등 무엇을 검색해도 내가 검색한 콘텐츠만 나오는 것이 아니라 그래프의 특성에 따라 다양한 콘텐츠들이 함께 노출될 거예요!
트리
👩👧👦 지휘계통(가족관계도) / 대진표
운동 경기나 체육대회 등에서 겨룰 차례를 정해 놓은 표를 보면 트리구조와 비슷한 것을 볼 수 있습니다.
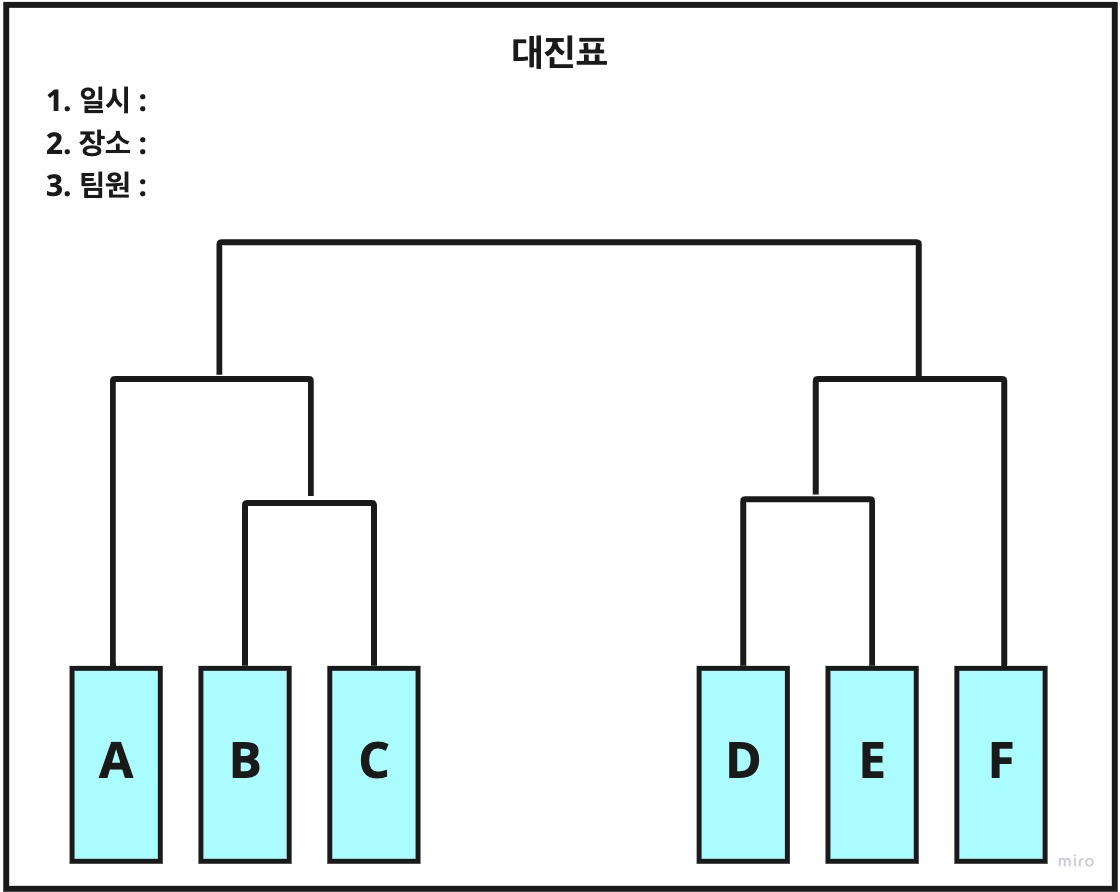
참고 이미지 대진표는 월드컵을 예로 생각해 보면 쉽게 트리와 비슷하다는 것을 알 수 있습니다.
또한 위와 비슷한 구조인 지휘계통에도 사용하는데 가족관계도를 떠올리면 쉽게 이해하실 수 있습니다.📂 파일 시스템
컴퓨터의 파일시스템을 보면 트리구조로 구성되어있다는 것을 알 수 있습니다.
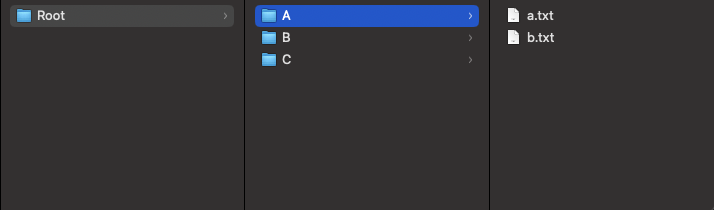
참고 이미지 Root 폴더 아래 A, B, C 폴더가 자식 노드로 있고 A 폴더 아래에는 a.txt, b.txt 파일 노드가 존재합니다.
B와 C 폴더 아래에는 자식 노드가 존재할 수도 하지 않을 수도 있습니다.👀 그 외
- HTML Tag 구조
- HTML에 대해 아직 모르실 수 있으니 제가 정리해놓은 링크에 가시면 HTML 태그 구조를 포함하여 웹의 전체적인 렌더링 과정에 대한 설명을 통해 더 쉽게 이해할 수 있으며 트리구조와의 연관성까지 자세히 알 수 있습니다.
👉🏻 알아보러가기
- HTML에 대해 아직 모르실 수 있으니 제가 정리해놓은 링크에 가시면 HTML 태그 구조를 포함하여 웹의 전체적인 렌더링 과정에 대한 설명을 통해 더 쉽게 이해할 수 있으며 트리구조와의 연관성까지 자세히 알 수 있습니다.
- 도 → 시군구 → 읍면동 의 주소 체계
- DBMS (Database Management system)
- 검색 엔진
- 검색 엔진은 그래프에서 나왔는데 트리에서 왜 또 쓰이지? 언제 사용한다는 거야? 라는 생각이 들 것 같습니다! 그래프에서 사용된 것처럼 사용될 수도 있지만 여기서 말하는 검색 엔진은 그래프에서 예로 들었던 것과는 조금 다릅니다.
말 그대로 “검색 엔진" 자체에 대한 알고리즘입니다.
이 트리구조는 종류가 여러 가지 있는데 검색과 연관 지어 이해할 수 있도록 정리해놓은 자료가 있으니 아래의 링크에서 검색 엔진에 대한 트리구조를 자세히 알아볼 수 있습니다.
👉🏻 알아보러가기
- 검색 엔진은 그래프에서 나왔는데 트리에서 왜 또 쓰이지? 언제 사용한다는 거야? 라는 생각이 들 것 같습니다! 그래프에서 사용된 것처럼 사용될 수도 있지만 여기서 말하는 검색 엔진은 그래프에서 예로 들었던 것과는 조금 다릅니다.
'개발' 카테고리의 다른 글
비동기처리 작동 원리, Microtask Queue & Task Queue (0) 2022.04.02 CSR VS SSR / 크로스 브라우징 QA (0) 2022.04.01 OOP와 함수형 프로그래밍 QA (0) 2022.04.01 클로저와 호이스팅에 대한 QA (0) 2022.03.31 최적화에 대해 알아보며 나한테 묻는 QA (0) 2022.03.31