Hash Table (해시 테이블)

 

Hash Table ( 해시 테이블 )

 

해시 테이블(해시 맵이라고도 합니다.)은 연관배열 구조를 이용하여 키(key)에 결과 값(value)을 저장하는 자료구조 입니다.

해시 테이블은 키를 저장할 때에 메모리 공간을 덜 사용할 수 있도록, 키를 "해시 함수"(Hash Function)라는 함수를 통해 특정 숫자값의 인덱스로 변환합니다. 해시 테이블은 필요할 때에만 메모리 크기를 늘리고, 가능한 작은 크기를 유지합니다.

 

 

 

연관배열 구조( associative array )란

 

키(key) 1개와 값(value) 1개가 1:1로 연관되어 있는 자료구조 입니다. 따라서 키(key)를 이용하여 값(value)을 도출할 수 있습니다.

 

연관배열 구조는 다음의 명령들을 지원하고 이 명령들은 해시테이블에서도 동일하게 적용됩니다.

• 키(key)와 값(value)이 주어졌을 때, 연관 배열에 그 두 값(key & value)을 저장하는 명령
• 키(key)가 주어졌을 때, 연관되는 값(value)을 얻는 명령
• 키(key)와 새로운 값(value)이 주어졌을 때, 원래 키에 연관된 값(value)을 새로운 값(value)으로 교체하는 명령
• 키(key)가 주어졌을 때, 그 키(key)에 연관된 값(value)을 제거하는 명령

 

 

 

해시 테이블의 구조 (Hash Table Data Structure)

 

 

해시 테이블은 키(key), 해시함수(Hash Function), 해시(Hash), 값(key), 저장소(Bucket, slot)로 이루어져 있습니다.

 

키(key)는 해시함수(HashFunction)을 통해 해시(hash)로 변경이 되며 해시는 값(value)과 매칭되어 저장소에 저장이 됩니다.

 

• 키(key) : 고유한 값이고 해시 함수의 input값이 됩니다. 이 상태로 최종 저장소에 저장이 되면 다양한 길이 만큼의 저장소를 구성해 두어야 하기 때문에 해시 함수로 값을 바꾸어 저장이 되어야 공간의 효율성을 추구할 수 있습니다.
  
  
• 해시함수(Hash Function) : 키를 해시로 바꿔주는 역할을 합니다. 다양한 길이를 가지고 있는 키를 일정한 길이를 가지는 해시로 변경하여 저장소를 효율적으로 사용할 수 있도록 도와줍니다. 다만, 서로 다른 키가 같은 해시가 되는 경우를 해시 충돌(Hash Collision)이라고 하는데, 해시 충돌을 일으키는 확률을 최대한 줄이는 함수를 만드는 것이 중요합니다.
  
  
• 해시(Hash) : 해시 함수의 결과물이며, 저장소에서 값과 매칭되어 저장됩니다.
  
  
• 값(value) : 저장소에 최종적으로 저장되는 값으로 키와 매칭되어 저장, 삭제, 검색, 접근이 가능해야 합니다.

 

 

즉, 해시 함수는 키를 바탕으로 해시 주소를 생성하고, 이 해시 주소가 배열로 구현된 해시 테이블의 인덱스가 됩니다.

이 인덱스로 해당 위치에 배열을 저장하거나 삭제, 탐색할 수 있습니다.

위의 그림처럼 계산된 해시 주소를 통해  ( bucket에 접근할 때의 값 )을 저장하고, 이 저장되는 공간을 bucket이나 slot이라고 합니다.

 

 

 

 

Insert (저장)

 

 

출처 : https://www.geeksforgeeks.org/implementing-hash-table-open-addressing-linear-probing-cpp/

 

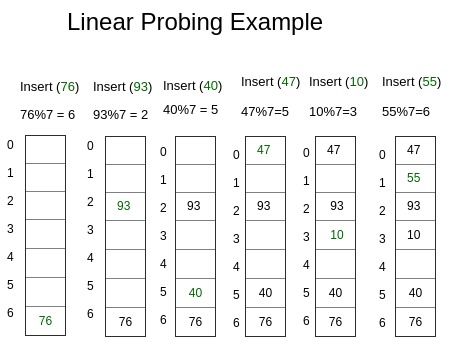
해시 테이블에서 자료를 저장하기 위해서는 해시 함수(Hash Function)로 키를 해시로 변경해야 합니다. 

위의 사진처럼 해시 함수가 input key를 7로 나눈 나머지로 변경해서 출력했을 때, 키는 "76" 해시는 "6"입니다.

그러면 미리 준비해놓은 0, 1, 2, 3, 4, 5, 6의 저장소 중에 맞는 해시 값을 찾아 해당 값을 저장하게 됩니다.

 

해시 함수로 해시를 산출하는 과정에서 서로 다른 키가 같은 해시로 변경되는 문제가 발생할 수 있는데, 이는 키와 값이 1:1로 매칭되어야 하는 규칙에 어긋나는 것 즉, 해시 충돌이 발생하는 것이고 이 문제들을 해결하면서 저장되어야 합니다.

 

Insert Big-O

저장 단계의 시간 복잡도는 O(1)입니다. 키는 고유하며 해시함수의 결과로 나온 해시와 값을 저장소에 넣기만 하면 되기 때문입니다.

( 이 때, 해시함수의 시간 복잡도는 함께 고려하지 않습니다.)

하지만 해시 충돌로 인해 모든 저장소들의 값을 찾아봐야 하는 경우도 있기 때문에 이런 경우에는 O(n)이 될 수 있습니다.

 

 

 

 

Delete (삭제)

 

저장되어 있는 값을 삭제할 때에는 저장소에 hash와 value가 함께 저장되어 있으므로 해당 키와 매칭되는 값을 찾아서 함께 삭제하면 됩니다. 

 

Delete Big-O

삭제 단계의 시간 복잡도는 O(1)입니다. 키는 고유하며 해시함수의 결과로 나온 해시에 매칭되는 값을 삭제 하기만 하면 되기 때문입니다.

(이 때, 해시함수의 시간복잡도는 함께 고려하지 않습니다.)

Insert Big-O와 마찬가지로 해시 충돌로 인해 모든 저장소들의 값을 찾아봐야 하는 경우도 있기 때문에 이런 경우에는 O(n)이 될 수 있습니다.

 

 

Search Big-O

저장 단계의 시간 복잡도는 O(1)입니다. 키는 고유하며 해시함수의 결과로 나온 해시에 매칭되는 값을 찾기만하면 되기 때문입니다.

( 이 때, 해시함수의 시간 복잡도는 함께 고려하지 않습니다. )

저장 단계도 마찬가지로 해시 충돌로 인해 모든 저장소들의 값을 찾아봐야 하는 경우도 있기 때문에 이런 경우에는 O(n)이 될 수 있습니다.

 

 

 

 

Hash Collision ( 해시 충돌 )과  해시 충돌 해결 방법(Chaining)

 

해시테이블은 Insert, Delete, Search 과정에서 모두 평균적으로 O(1)의 시간 복잡도를 가지고 있기 때문에 자료구조의 효율성 측면에서 큰 장점이 될 수 있습니다. 하지만 자료구조는 장점만 있는게 아니라 단점도 존재하듯이 해시 테이블은 단점도 가지고 있습니다.

 

 

위의 사진을 보시면 key로 들어간 Sandra가 기존에 있던 John과 hash가 같아서 충돌이 일어났습니다. 이런 현상을 바로 Hash Collision (해시 충돌)이라고 합니다.

 

해시 충돌은 필연적으로 나타날 수 밖에 없습니다. n + 1개의 비둘기가 n개의 비둘기 집에 들어간다면 적어도 1개 이상의 비둘기 집에 2마리 이상의 비둘기가 있을 것입니다.

 

해시 테이블의 비둘기 집의 원리

해시 함수는 결정론적으로 작동해야 하며, 따라서 두 해시값이 다르다면 그 해시값에 대한 원래 데이터도 달라야 한다. 비둘기집 원리란 n+1개의 물건을 n개의 상자에 넣을때 적어도 어느 한 상자에는 두 개 이상의 물건이 들어 있다는 원리를 말한다.

출처 : 위키백과 - 비둘기집 원리

 

 

그렇다면 이러한 해시 충돌을 처리하는 방법중 하나인 Chaining에 대해서 알아보도록 하겠습니다.

 

 

Collision Resolution

 

1. Separate Chaining (Chaining)

 

 

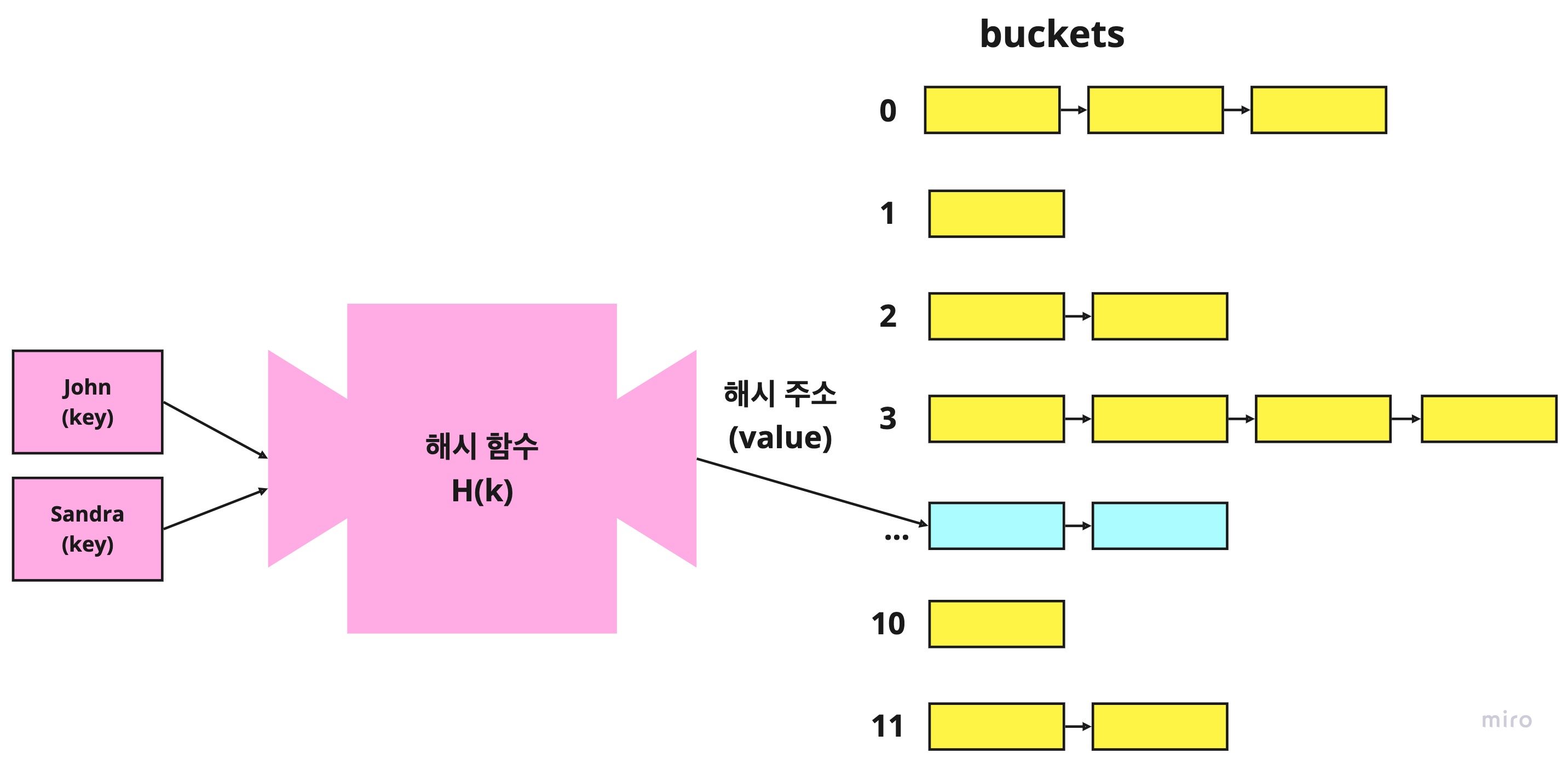
체이닝은 해시 테이블의 하나의 위치에 여러 개 항목을 저장할 수 있게 하는 구조로 설계합니다.

연결 리스트를 이용해서 구현한 것중에 하나로 Linked List와 유사한 구조로 체이닝을 구현할 수 있습니다.

 

Sandra가 들어가는데 충돌이 일어나니 기존에 있던 John의 값에 연결시켰습니다. 

체이닝 (chaining)은 자료 저장 시, 저장소에서 충돌이 일어나게 되면 해당 값을 기존 값과 연결시키는 기법입니다.

 

위의 사진에서 보시면 Sandra를 저장할 때 충돌이 일어났고, 기존에 있던 John에 연결시켰습니다.

이 때, 연결 리스트(Linked List)에서 사용 된 다음(next)에 저장된 자료를 기존의 자료 다음에 위치시키는 자료구조를 이용합니다.

 

 

Chaining의 장점과 단점

 

장점	단점
1. 한정된 저장소를 효율적으로 사용할 수 있습니다.	1. 한 해시에 자료들이 계속해서 연결된다면 검색 효율이 낮아질 수 있습니다.
2. 상대적으로 적은 메모리를 사용하기 때문에 미리 공간을 잡아 놓을 필요가 없습니다.	2. 외부 저장 공간 작업을 추가적으로 해줘야 합니다.
3. 해시 함수를 선택하는 중요성이 상대적으로 적습니다.	3. 외부 저장 공간을 사용합니다.

 

 

Chaining 시간 복잡도 (Big-O)

 

복잡도를 계산하기 전, 한 가지를 추가하자면 해시 테이블의 저장소(bucket)의 길이를 "n", 키의 수를 "m" 이라고 가정했을 때, 평균적으로 저장소에서 1개의 hash당 ( m / n )개의 키가 들어 있습니다. 이를 "a"라고 정의합니다.

// 1개의 hash당 평균적으로 a개의 키가 들어있다.
m / n = a 

 

 

 

 

※ Hash Table Data Structure의 단점

 

• 순서가 있는 배열에는 어울리지 않습니다.
  
  : 상하관계가 있거나, 순서가 중요한 데이터의 경우 Hash Table은 어울리지 않습니다. 순서와 상관없이 key만을 가지고 hash를 찾아 저장하기 때문입니다.
  
  
• 공간 효율성이 떨어집니다.
  
  : 데이터가 저장되기 전에 미리 저장공간을 확보해 놓아야 합니다. 공간이 부족하거나 아예 채워지지 않은 경우가 생길 가능성이 있습니다.
  
  
• Hash Function의 의존도가 높습니다.
  
  : 평균 데이터 처리의 시간 복잡도는 O(1)이지만, 이는 해시 함수의 연산을 고려하지 않은 결과입니다. 해시 함수가 매우 복잡하다면 해시테이블의 모든 연산의 시간 효율성은 증가할 수 밖에 없을 것입니다.

 

 

해시 테이블은 키를 가지고 빠르게 value에 접근하고 조작할 수 있는 장점이 있어서 많이 사용됩니다. 예를 들어 주소록 저장형태의 경우 이름-전화번호의 매칭을 이용하여 데이터를 처리하는것과 같습니다.