Tree와 Binary Search Tree
Tree
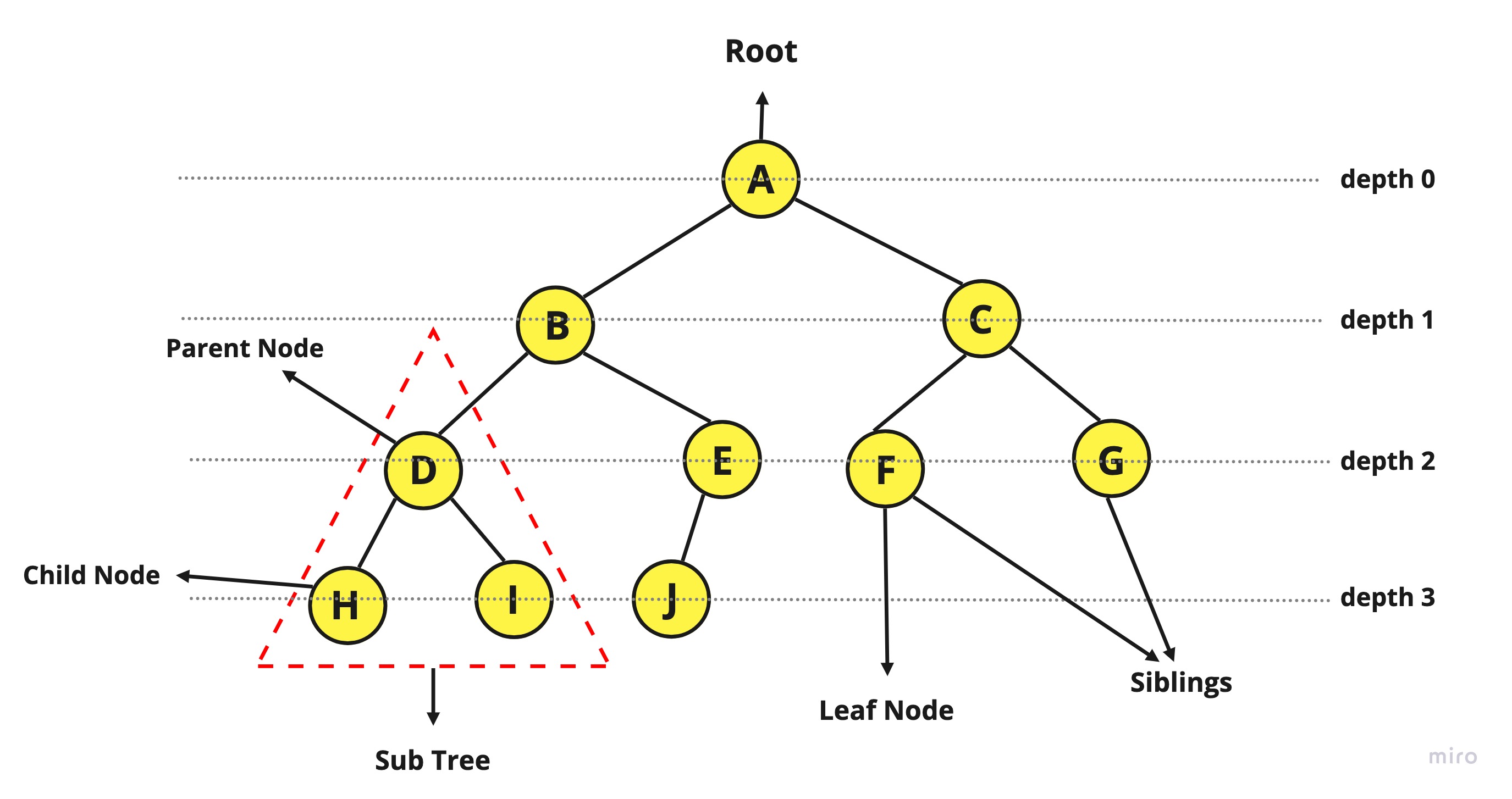
트리는 노드로 구성된 계층적 자료구조입니다. 최상위 노드(루트)를 만들고, 루트 노드의 child를 추가하고, 그 child에 또 child를 추가하는 방식으로 트리 구조를 구현할 수 있습니다.
Array, Linked List, Stack, Queue는 라인처럼 생긴 일직선 데이터 구조인데 Tree는 부모 자식 관계를 가지는 구조입니다.
Tree는 계층적 자료구조라고 했는데 이 것을 가능하게 한 것은 노드가 하나 이상의 child를 갖기 때문입니다.
노드중에는 부모를 아는경우도 있고 자식만 아는 경우도 있습니다. 또한 어떠한 순서에 의해서 데이터가 관리되는 경우도 있고, 데이터가 마구 섞여있는 경우도 있습니다.
※ 트리의 용어 정리
- 루트 노드 (Root) : 부모가 없는 노드, 트리는 하나의 루트노드만을 가집니다.
- 단말 노드 (Leaf) : 자식이 없는 노드, '말단 노드' 또는 '잎 노드' 라고도 부릅니다.
- 내부 노드 : 단말 노드가 아닌 노드.
- 간선 (Edge) : 노드를 연결하는 선. (link, branch 라고도 부릅니다)
- 형제 (Sibling) : 같은 부모를 가지는 노드
- 노드의 크기 (Size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이 (Depth) : 루트에서 어떤 노드에 노달하기 위해 거쳐야 하는 간선의 수
- 노드의 레벨 (level) : 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수 (degree) : 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- 트리의 차수 (degree of tree) : 트리의 최대 차수
- 트리의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
Binary Tree와 Binary Search Tree
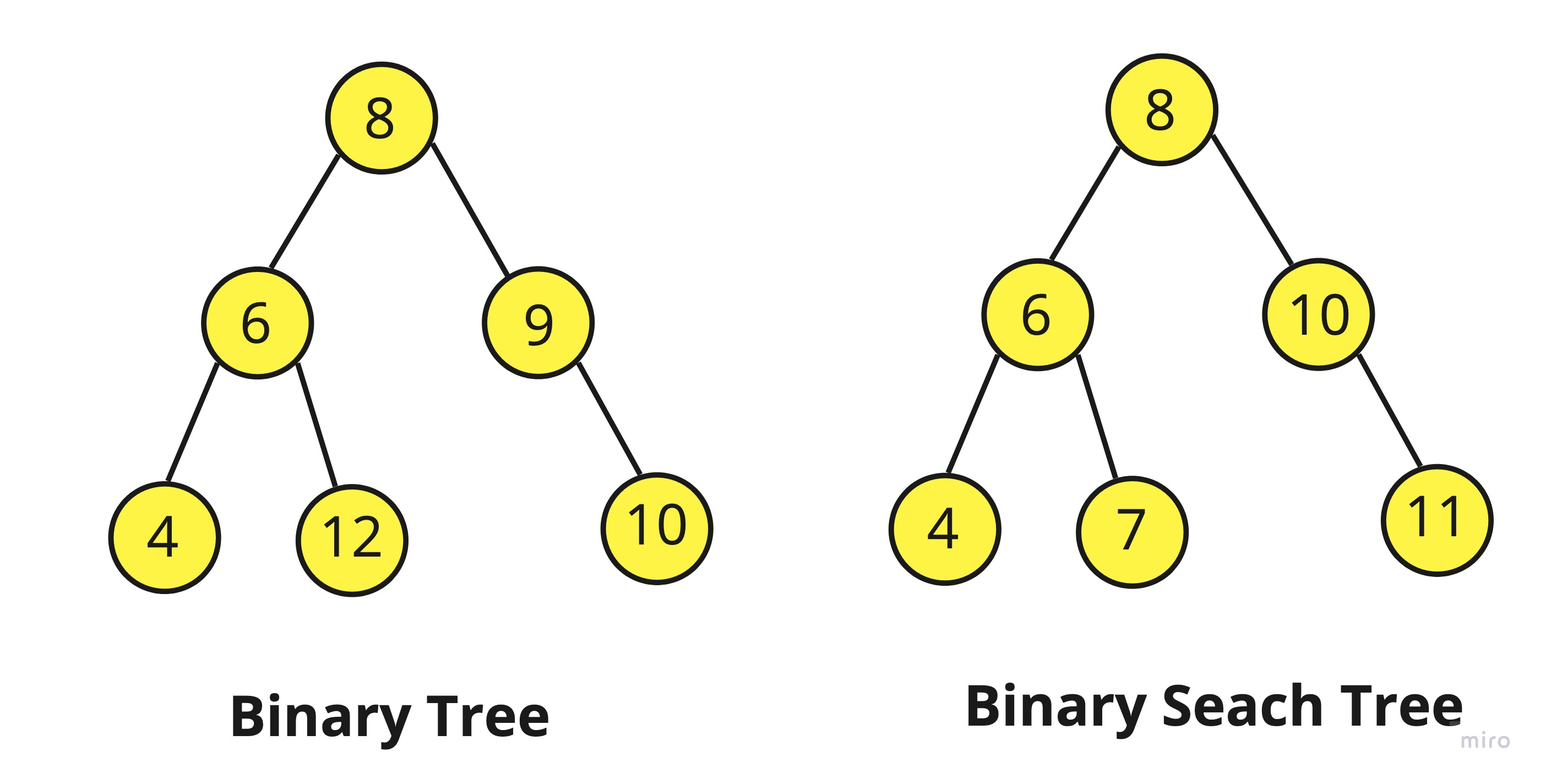
Binary Tree는 다른 조건 없이 노드의 child가 최대 2개씩만 붙어 있다면 Binary Tree입니다.
Binary Search Tree는 안에 있는 데이터가 왼쪽 노드와 그 이하 child노드들은 현재 노드보다 작아야하고, 오른쪽 노드와 그 이하 child노드들은 현재 노드보다 커야 합니다.
그렇기 때문에 Binary Search Tree는 노드를 보고 해당 노드의 값보다 작은 값을 찾고 싶으면 왼쪽에서 찾으면 되고, 큰 값을 찾고 싶다면 오른쪽에서 찾을 수가 있기 때문에 찾고자 하는 값이 현재 노드보다 큰지, 작은지만 알면 쉽게 찾아낼 수 있습니다.
반면에 Binary Tree는 이러한 규칙이 없기 때문에 데이터가 섞여 있습니다.
Balance ( 밸런스 )
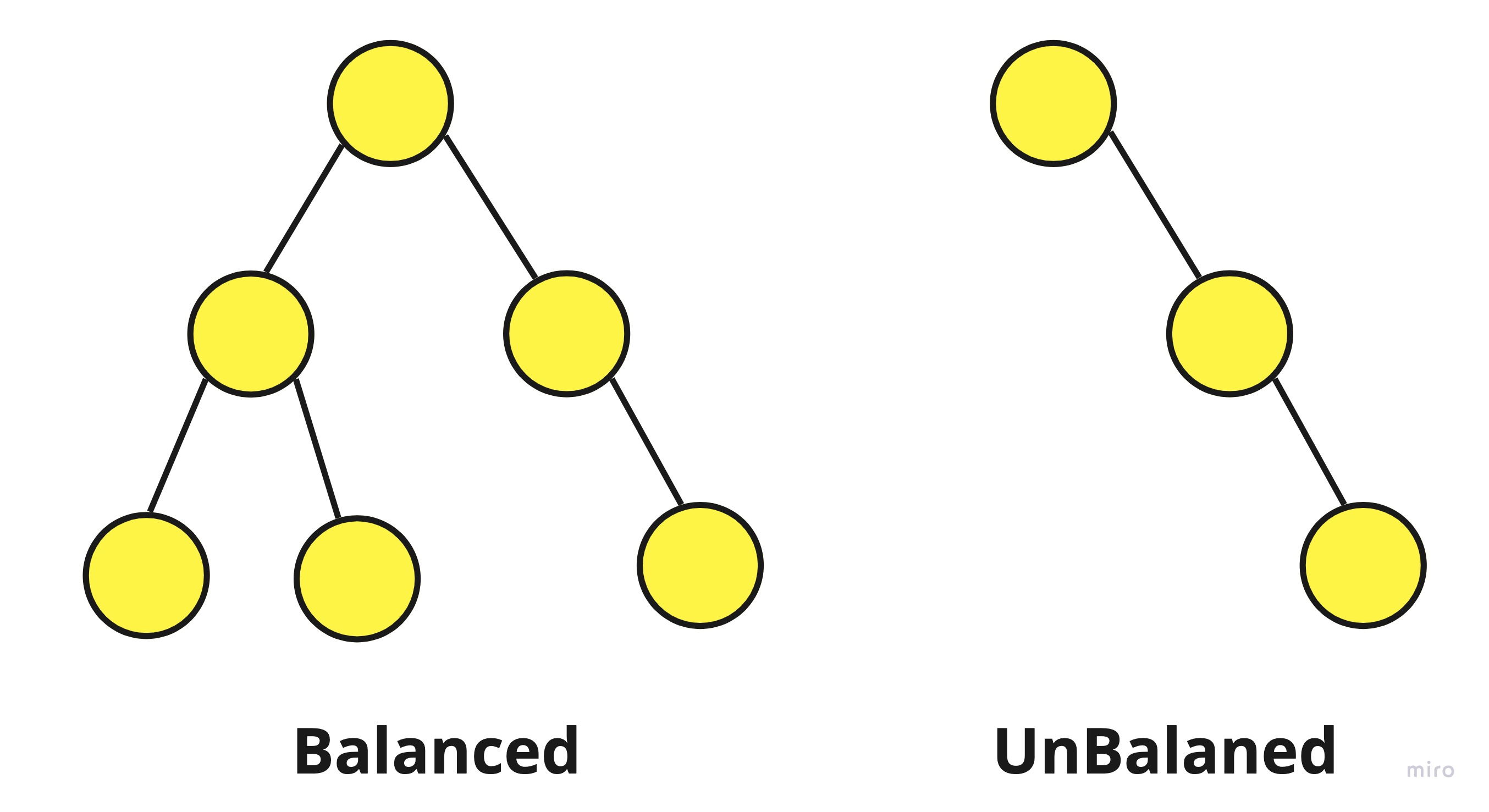
트리에서 밸런스가 맞다 안맞다의 기준은 왼쪽 오른쪽 노드의 개수가 정확하게 일치해야 하는 것은 아닙니다.
너무 지나치게 치우쳐 있지만 않다면 밸런스가 맞다 라고 표현합니다.
위 그림을 보면 Balanced의 트리에서 최상위 루트를 기준으로 왼쪽과 오른쪽의 노드 개수가 일치하지 않지만 밸런스가 맞다고 봅니다.
UnBalanced 의 트리에서는 오른쪽으로만 노드가 치우쳐 있기 때문에 언밸런스하다고 표현한 것입니다.
Binary Search Tree의 세가지 종류
1. Complete Binary Tree ( 완전 이진 트리 )

완전 이진 트리는 위의 그림에서 오른쪽 그림처럼 모든 노드들이 레벨별로 왼쪽부터 채워져 있다면 완전 이진 트리입니다.
즉, 트리를 만들다 보면 레벨이 생기는데 마지막 레벨을 제외한 모든 서브트리의 레벨이 같아야 하고 마지막 레벨은 왼쪽부터 채워져 있다면 완전 이진 트리인 것입니다.
왼쪽 그림을 보시면 서브트리의 레벨은 맞는데 마지막 레벨을 보면 왼쪽부터 채워져 있지 않습니다.
따라서 왼쪽 그림은 완전 이진트리가 아닌 그냥 이진트리인 것입니다.
2. Full Binary Tree ( 정 이진 트리 )
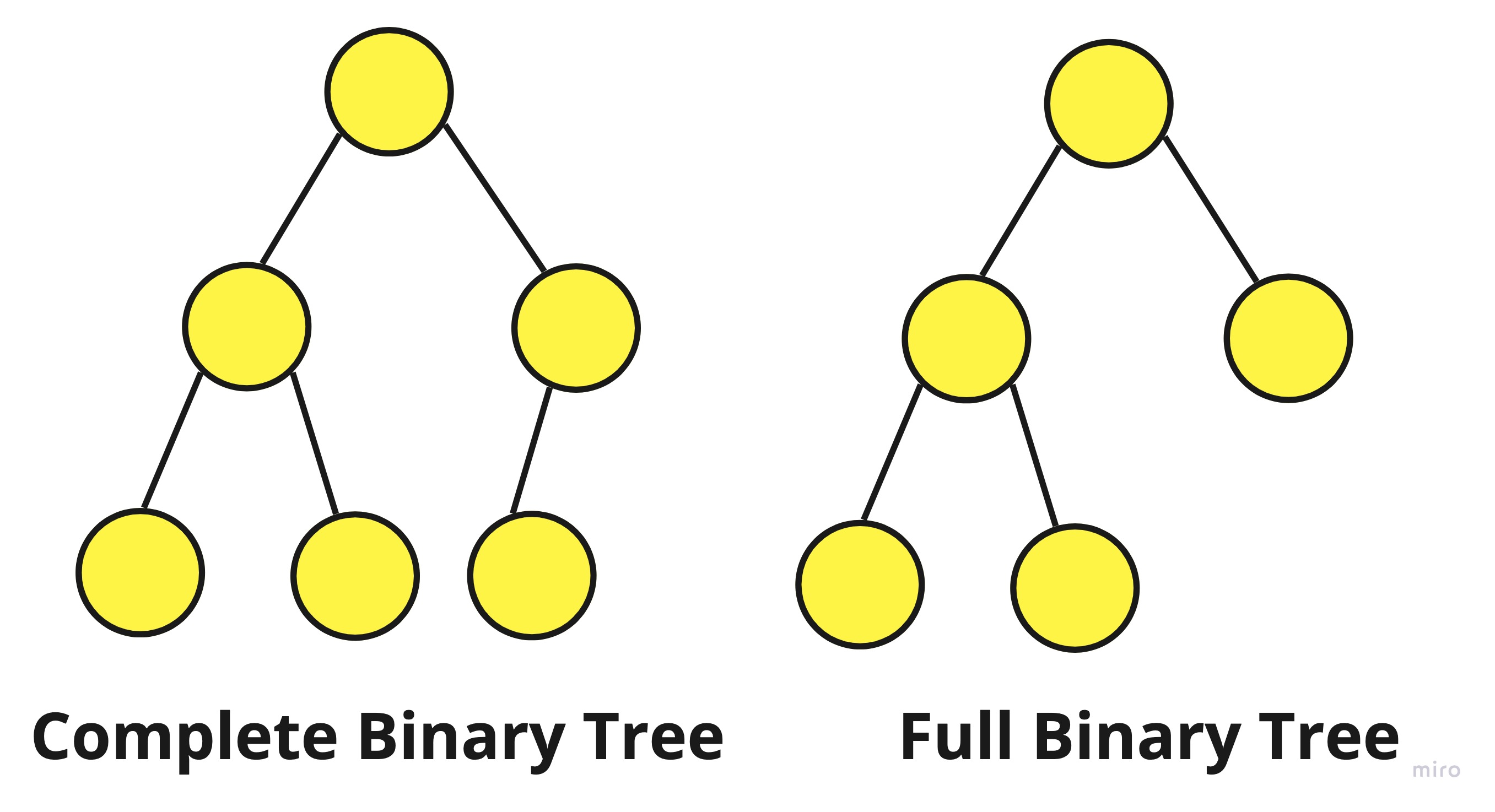
왼쪽의 완전 이진 트리처럼 하나의 child노드를 가진 노드가 하나도 존재하지 않았을 경우에만 Full Binary Tree 라고 합니다.
Full Binary Tree가 되려면 오른쪽 그림처럼 그 안에 노드들이 child를 갖지 않으려면 하나도 없어야 하고 갖으려면 두개를 가져야만 합니다.
3. Perfect Binary Tree ( 포화 이진 트리 )
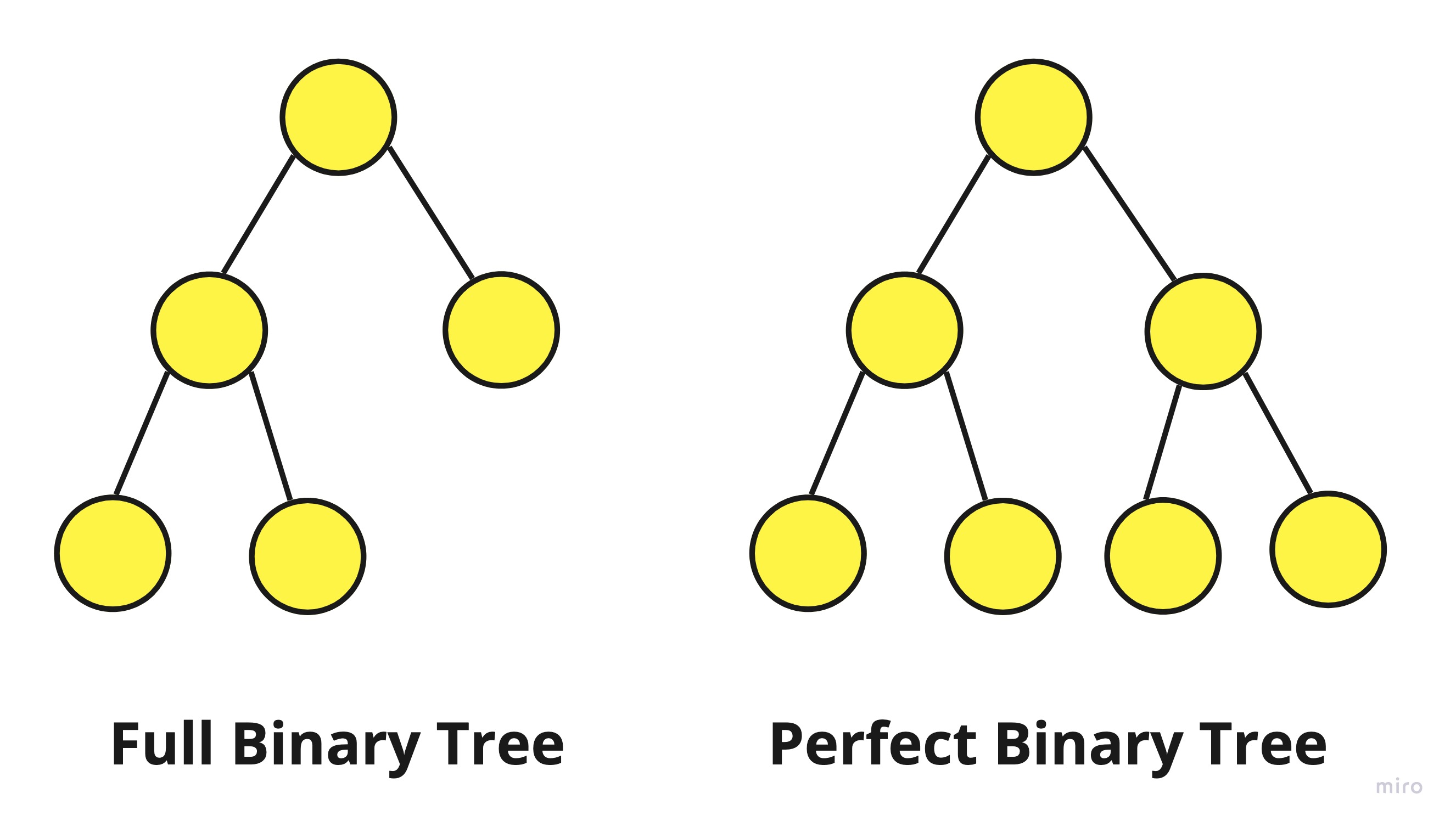
Perfect Binary Tree는 양쪽으로 빈공간 없이 모든 노드가 두개의 자식을 가지고 레벨도 정확하게 딱 떨어지는 구조입니다.
완벽한 피라미드 구조를 형성하고 있습니다.
한국에서는 Perfect Binary Tree를 포화 이진 트리라고 하는데 번역을 하면 Full Binary Tree라고 나와서 굉장히 헷갈릴 수 있습니다.
Perfect Binary Tree를 정확하게 구별할 수 있는 방법은 레벨의 갯수를 n이라고 가정할 때 2^n-1 ( 2의 n제곱 - 1 ) 개의 노드를 갖는 것이 Perfect Binary Tree입니다.
Binary Search Tree의 데이터 가져오는 방법
이진 탐색 트리가 주어졌을 때, 트리의 데이터를 가져오는 방법에는 크게 세가지로 나뉩니다.
- Inorder Traversal (중위 순회) : 좌 -> 부모 -> 우
- Preorder Traversal (전위 순회) : 부모 -> 좌 -> 우
- Postorder Traversal (후위 순회) : 좌 -> 우 -> 부모
1. Inorder ( 중위 순회 )

Inorder는 루트노드를 시작으로 노드의 왼쪽이 먼저 그다음이 루트, 그다음이 오른쪽 노드 입니다.
출력 결과를 설명하자면 다음과 같습니다.
1부터 시작해서 왼쪽으로 먼저가고 child가 있으니 한번 더 왼쪽으로 갑니다. 4는 더이상 child노드가 없으므로 4를 출력합니다.
그리고 다시 루트로 올라가서 루트인 자기 자신 2를 출력하고 오른쪽으로 가서 5를 출력합니다.
출력하고서 루트로 이동을하면 2는 이미 출력했기 때문에 무시하고 그 위로 올라가서 1을 출력하고 마지막으로 3을 출력합니다.
2. Preorder ( 전위 순회 )

Preorder는 자기자신을 먼저 출력하고 그다음이 왼쪽, 그다음으로 오른쪽을 순회하는 것이 Preorder의 방법입니다.
출력 결과를 설명해보자면 다음과 같습니다.
1부터 시작해서 자기 자신인 1을 먼저 출력하고 왼쪽으로 가서 child노드로 가기전에 자기 자신을 먼저 출력하기 때문에 2를 출력한 후에 child노드로 들어가 4를 출력합니다. 4에는 더이상 child노드가 없으므로 다시 위로 올라가서 오른쪽노드로 이동하여 5를 출력합니다.
그리고서 다시 위로 올라가는데 2와 1은 이미 출력했으므로 3을 마지막으로 출력하게 됩니다.
3. Postorder ( 후위 순회 )
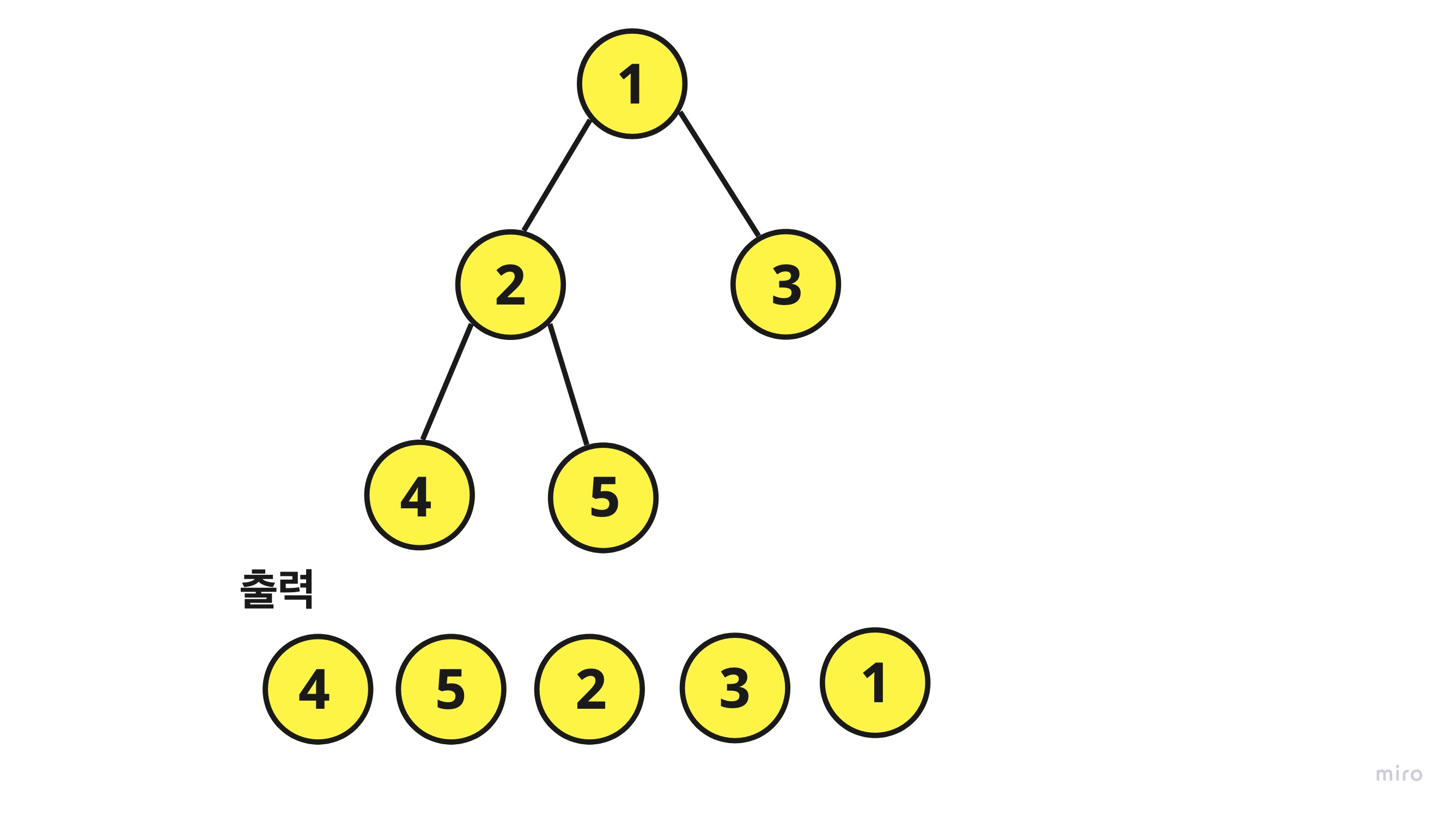
Postorder는 왼쪽노드를 먼저 출력하고 그 다음에는 오른쪽노드를 출력하고 마지막으로 자기 자신을 출력합니다.
출력 결과를 설명해보자면 다음과 같습니다.
먼저 1부터 시작해서 왼쪽노드로 들어가서 child노드가 더이상 없는 4까지 들어간 후에 4를 출력합니다.
그리고서 2로 올라와서 자기 자신을 출력하기 전에 오른쪽 노드로 들어가 5를 출력하고 그 다음에 2로 올라와서 자기 자신을 출력한 후, 1로 올라와서 자기 자신을 출력하기 전에 왼쪽은 다 출력됬으니 오른쪽으로 가서 3을 출력하고 마지막으로 자기 자신인 1을 출력하고 마무리합니다.